[공업수학] 6.1 라플라스 변환, 라플라스 변환표, s-이동정리

일상생활 작성
작성일 2025.03.23 21:58

126 조회
0 추천
목록

글수정 글삭제

안녕하세요, 여러분! 오늘도 인생꿀팁 블로그에 찾아와 주셔서 감사합니다. 오늘은 공업수학의 핵심 개념인 ‘라플라스 변환’에 대해 자세히 살펴보겠습니다. 라플라스 변환은 미분방정식을 해결하는 데 있어 매우 유용한 도구인데요. 그동안 이 개념에 대해 궁금했던 점이 있으셨다면 이 글을 통해 자세히 알아보실 수 있을 거예요.

[ 회로이론 ]전기에서 자주나오는 라플라스 변환 표

라플라스 변환의 기본 개념

라플라스 변환(Laplace Transform)은 공업수학에서 굉장히 중요한 도구인데요. 시간 영역에서의 문제를 주파수 영역으로 변환해줘서, 복잡한 미분 방정식을 더 쉽게 해결할 수 있게 도와줘요. 주로 전기 회로나 제어 시스템에서 많이 사용되죠.

라플라스 변환의 정의는 다음과 같아요:

[ \mathcal{L}{f(t)} = \int_{0}^{\infty} e^{-st} f(t) , dt ]

여기서 ( \mathcal{L} )은 라플라스 변환을 의미하고, ( f(t) )는 시간에 대한 함수, ( s )는 복소수 변수를 나타냅니다.

라플라스 변환은 실수 함수 f(t)를 복소수 함수 F(s)로 변환하는 기법입니다. 이를 통해 미분방정식을 대수방정식으로 변환할 수 있어 문제 해결이 쉬워집니다. 라플라스 변환은 선형 시불변 시스템을 해석하는 데 널리 사용되며, 회로 이론, 제어 이론, 신호 처리 등 다양한 공학 분야에서 활용됩니다.

라플라스 변환 – 변환표

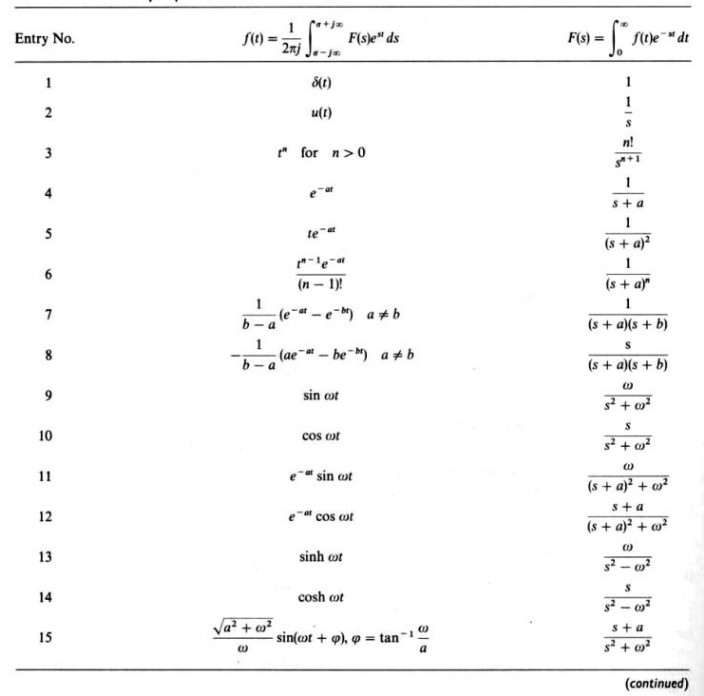
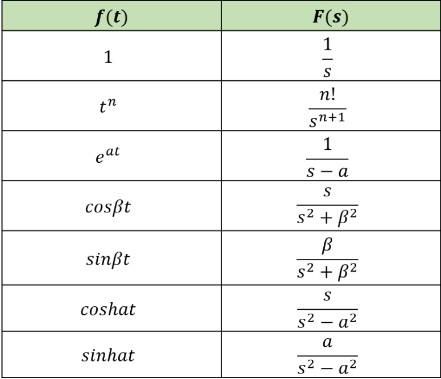
라플라스 변환표

라플라스 변환표는 다양한 함수들의 라플라스 변환 결과를 표로 정리해놓은 것인데요. 이를 통해 복잡한 계산을 빠르게 할 수 있어요. 예를 들어, 다음과 같은 기본 함수들의 라플라스 변환 결과를 기억해두면 유용해요:

( \mathcal{L}{1} = \frac{1}{s} )
( \mathcal{L}{t} = \frac{1}{s^2} )
( \mathcal{L}{e^{at}} = \frac{1}{s-a} )

이런 기본 변환 결과들을 알면, 복잡한 함수도 쉽게 변환할 수 있었답니다.

s-이동정리

s-이동정리(Shifting Theorem)는 라플라스 변환을 더 효율적으로 활용할 수 있게 해주는 중요한 정리 중 하나에요. 이 정리는 시간 영역에서의 함수가 특정 값만큼 이동했을 때, 주파수 영역에서의 변형을 설명해 줍니다.

s-이동정리의 공식은 다음과 같아요:

시간 이동: ( \mathcal{L}{f(t-a)} = e^{-as}F(s) )
주파수 이동: ( \mathcal{L}{e^{at}f(t)} = F(s-a) )

이를 통해 특정 함수가 시간이나 주파수 영역에서 이동했을 때, 라플라스 변환 결과가 어떻게 변하는지 쉽게 알 수 있어요.

실생활 활용 사례

저도 라플라스 변환을 처음 배울 때는 개념 이해가 쉽지 않았어요. 하지만 실제 문제를 풀어보면서 점차 익숙해졌습니다. 예를 들어 RC 회로 문제를 풀 때 라플라스 변환을 활용하면 미분방정식을 쉽게 해결할 수 있었죠. 또한 제어 시스템 설계 시에도 라플라스 변환이 큰 도움이 되었습니다.

회로이론 _라플라스 변환표