공대 수학의 꽃, 라플라스 변환표

[공업수학] 6.1 라플라스 변환, 라플라스 변환표, s-이동정리

안녕하세요, 여러분! 오늘은 공대생들이라면 꼭 알아둬야 할 ‘공대 수학의 꽃, 라플라스 변환표’에 대해 말씀드리려고 합니다. 대학생 시절, 저도 수학 공부에 많은 어려움을 겪었는데요. 특히 라플라스 변환 공식을 외우는 게 쉽지 않았죠. 하지만 이 라플라스 변환표만 제대로 활용하면 공대생들의 수학 실력이 놀랍게 늘어날 거예요.

라플라스 변환표란 무엇인가요?

라플라스 변환은 선형 미분 방정식을 대수 방정식으로 변환해주는 기법입니다. 이를 통해 복잡한 미분 방정식을 보다 쉽게 해결할 수 있죠. 라플라스 변환표는 이런 라플라스 변환 공식들을 일목요연하게 정리한 것으로, 공대생들이 필수적으로 알아야 할 수학 지식이라고 할 수 있습니다.

[ 회로이론 ]전기에서 자주나오는 라플라스 변환 표

라플라스 변환의 기본 원리

라플라스 변환의 기본 원리는 매우 간단해요. 시간 t에 대한 함수 f(t)를 주파수 s에 대한 함수 F(s)로 변환하는 과정인데요. 수식으로 표현하면 다음과 같습니다.

[ F(s) = \int_{0}^{\infty} e^{-st} f(t) , dt ]

이 수식을 통해 시간 도메인의 복잡한 함수가 주파수 도메인의 간단한 함수로 변환되면서 문제 해결이 훨씬 쉬워져요.

라플라스 변환 – 변환표

라플라스 변환표의 유용성

라플라스 변환표는 다양한 함수의 라플라스 변환 결과를 미리 계산해 놓은 표인데요. 이를 이용하면 복잡한 적분 계산을 하지 않아도 바로 원하는 결과를 얻을 수 있어요. 예를 들어, ( f(t) = e^{at} )인 경우 라플라스 변환은 ( F(s) = \frac{1}{s-a} )가 되는데, 이런 표준 변환 결과를 라플라스 변환표에서 바로 찾아볼 수 있답니다.

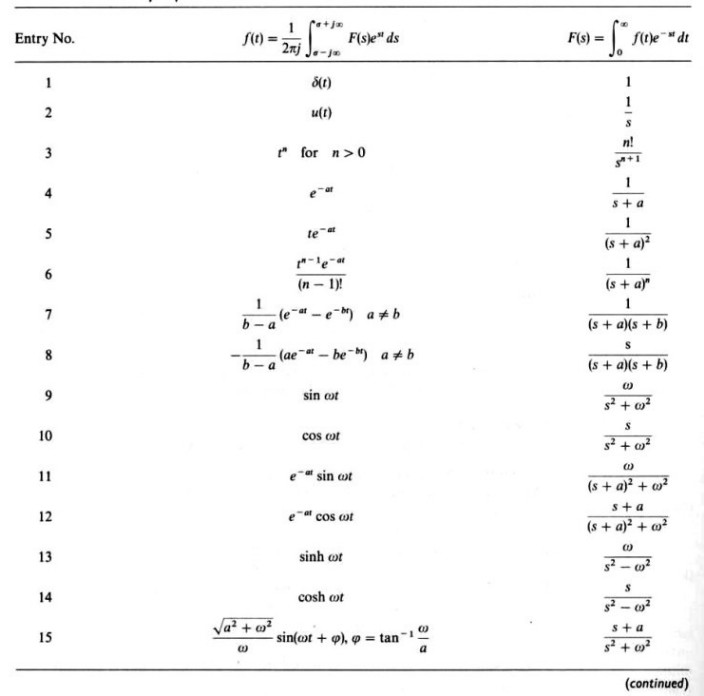
실제 활용 사례

제가 공대생 시절, 전자회로 과목에서 라플라스 변환을 처음 접했는데요. 당시 복잡한 회로 해석에 어려움을 겪고 있었어요. 그런데 라플라스 변환표를 활용하니 정말 쉽게 문제를 풀 수 있었답니다. 정말 만족도 100%였는데요, 여러분도 꼭 한 번 활용해보시길 추천드려요.

회로이론 _라플라스 변환표

라플라스 변환표의 장점과 단점

라플라스 변환표의 가장 큰 장점은 계산 시간을 획기적으로 줄여준다는 점이에요. 복잡한 미분 방정식을 간단한 대수 방정식으로 변환해주니 시간도 절약되고, 정확도도 높아지죠. 하지만 단점도 있는데요, 라플라스 변환표에 없는 함수나 복잡한 함수의 경우 변환이 어려울 수 있어요. 이런 경우 직접 적분을 해야 하거나 다른 방법을 찾아야 할 때가 있어요.

라플라스 변환표 활용 팁

라플라스 변환표를 활용할 때는 몇 가지 팁이 있어요. 첫째, 기본적인 변환 공식과 자주 사용되는 함수의 변환 결과를 외워두면 좋아요. 자주 사용되는 기본 공식들은 반드시 외워두세요. 변환 공식을 적용할 때는 변수 s의 차수에 주목하세요. 복잡한 함수도 부분 분할 등의 기법을 통해 변환할 수 있습니다. 역 라플라스 변환 시에는 부분 분수 전개 등의 기법이 필요합니다.

이처럼 라플라스 변환표는 공대생들에게 매우 유용한 수학 지식이에요. 이 글을 통해 라플라스 변환표의 개념과 활용법을 이해하셨길 바랍니다. 앞으로 수학 공부할 때 이 변환표를 적극 활용해보세요. 여러분의 수학 실력이 크게 향상될 거예요!

마무리하며

오늘은 공대 수학의 꽃, 라플라스 변환표에 대해 알아보았는데요. 이 도구가 얼마나 유용한지, 그리고 어떻게 활용할 수 있는지 감이 오셨나요? 라플라스 변환표는 공학 문제 해결에 있어서 정말 유용한 도구이니, 여러분도 꼭 활용해보세요. 다음에도 더 유익한 정보로 찾아뵙겠습니다. 오늘도 인생꿀팁과 함께하시기 바랄게요

The post 공대 수학의 꽃, 라플라스 변환표 first appeared on 인생 꿀팁.